Understanding Vectors

Several mathematical formulas can be used to determine if two vectors are similar. One of the most intuitive to visualize and understand is cosine similarity. Consider the following images that show three sets of graphs:

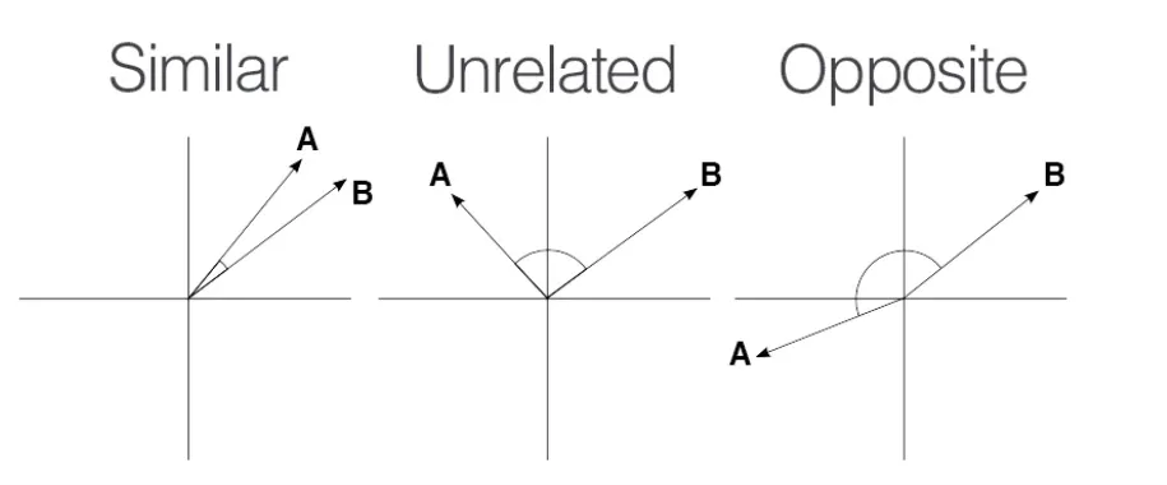
The vectors and are considered similar, when they are pointing close to each other, as in the first diagram. The vectors are considered unrelated when pointing perpendicular to each other and opposite when they point away from each other.

The angle between them, , is a good measure of their similarity. How can the angle be computed?

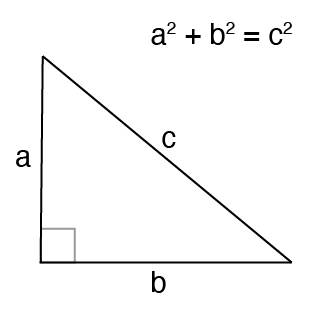
We are all familiar with the Pythagorean Theorem.

What about when the angle between a and b is not 90 degrees?

Enter the Law of cosines.

The following image shows this approach as a vector diagram:

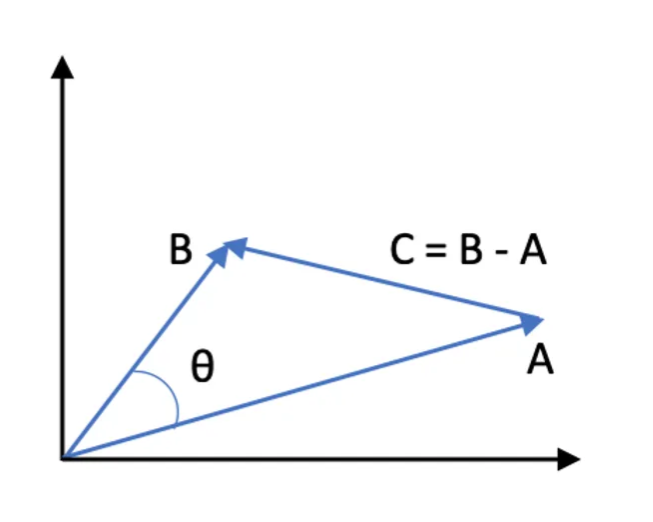
The magnitude of this vector is defined in terms of its components as:

The dot product between two vectors and is defined in terms of its components as:

Rewriting the Law of Cosines with vector magnitudes and dot products gives the following:

Replacing with gives the following:

Expanding this out gives us the formula for Cosine Similarity.

This formula works for dimensions higher than 2 or 3, though it is hard to visualize. However, it can be visualized to some extent. It is common for vectors in AI/ML applications to have hundreds or even thousands of dimensions.

The similarity function in higher dimensions using the components of the vector is shown below. It expands the two-dimensional definitions of Magnitude and Dot Product given previously to N dimensions by using Summation mathematical syntax.

This is the key formula used in the simple implementation of a vector store and can be found in the SimpleVectorStore implementation.